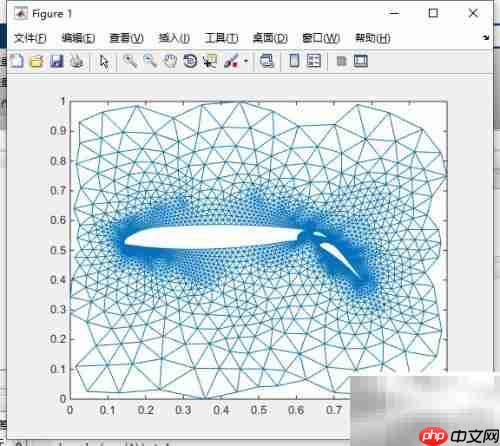
该案例呈现了美国航天局翼型的有限元网格模型,其中包含两个可动的后缘襟翼结构。
1、 相关数据存储于文件 AIRFOIL.MAT 中。
2、 网格坐标由4253组x与y值构成。
3、 数据中还包含一个索引数组,共12289对(i, j)值,用于描述网格点之间的连接关系。
4、 在命令窗口中键入相应指令:
5、 网格划分方法
6、 首先将所有x和y坐标值除以2的32次方,将其归一化至[0,1]区间。
7、 构建稀疏邻接矩阵,并确保其具备正定性质。
8、 在命令行中输入:
9、 按下回车执行操作。
10、 如图1所示。
11、 显示稀疏数据分布模式
12、 使用SPY函数可图形化展示矩阵A的稀疏结构,清晰反映非零元素的位置分布。
13、 在命令行输入对应命令:
14、 按回车键完成执行。
15、 如图2所示。
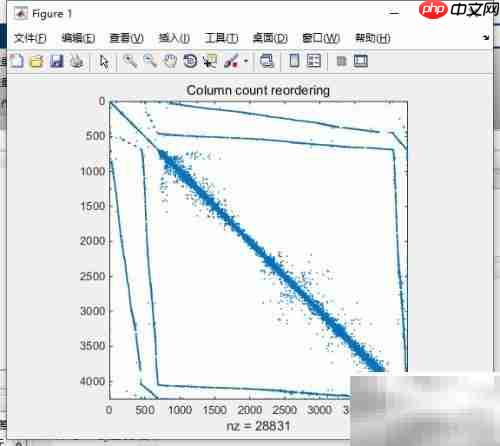
16、 采用反向Cuthill-McKee法进行对称矩阵重排
17、 SYMRCM函数基于逆向Cuthill-McKee算法对邻接矩阵实施重排序处理。
18、 调用r=SYMRCM(A)可获得置换向量r,使得重排后的矩阵A(r,r)的非零项更靠近主对角线,优化带宽结构。
19、 对细长型矩阵预先重排,有助于提升LU或Cholesky分解的计算效率与数值稳定性。
20、 该方法适用于对称及非对称矩阵A。
21、 输入如下命令:
22、 按回车确认运行。
23、 如图3所示。
24、 利用COLPERM进行对称重排序
25、 COLPERM返回排列向量j,使稀疏矩阵A的各列按非零元素数量升序排列。
26、 此方法常作为LU分解前的预处理步骤,即先对A的列重排再进行分解运算。
27、 在命令行输入:
28、 按下回车键执行命令。
29、 如图4所示。
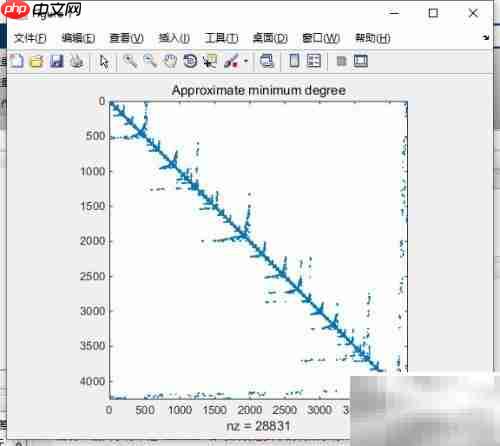
30、 符号对称重排技术
31、 实现近似对称的最小度数重排序策略。
32、 对于对称正定矩阵S,调用p=symmd(S)可得置换向量p,使得重排后的矩阵S(p,p)在进行Cholesky分解时产生更少的填充项,保持更高稀疏性。
33、 某些对称不定矩阵亦可适用symmd方法进行处理。
34、 输入以下命令行指令:
35、 按回车键确认执行。
36、 如图5所示。

 路由网
路由网